Última revisión de 18:40 27 feb 2019

[editar] Tier1 variables

These diagnostics are required by CORDEX, but they are not mandatory. They have been also included as a way to fulfill all the CORDEX requirements. These variables require the setting of the pre-compilation flag CDXWRF to 1 and performing some complementary modifications in the module’s Registry file registry.cordex. See section 2.3 for more details.

[editar] zmlagen: generic boundary layer height

Instantaneous Planetary Boundary Layer (PBL) height is a clear example of model dependence and even scheme dependence of how a diagnostic is computed. Each PBL scheme has its own assumptions and ‘zmla’ is computed in a scheme-dependent specific way.

In order to overcome the model/scheme dependence, we implemented a generic formulation for calculating the PBL height as it was done in (García-Díez et al., 2013) after (Nielsen-Gammon et al., 2008). The method consists in defining the height of the PBL as the first level in the mixed layer (ML) where potential temperature exceeds the minimum potential ML temperature by more than 1.5 K. It has been implemented using the definitions given below:

1. Mixed layer depth (MLD) is defined as the model level (k_MLD) starting from the second model level at which the variation of the mixing ratio (QVAPOR(k), normalized with its value at the first level) exceeds some predefined threshold value (QVAPOR(1)): 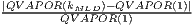> δQVAPOR (here applied a δQVAPOR = 0.1)
2. Within the MLD the value with the minimum potential temperature is taken as: θmin(MLD = min[θ(1), ..., θ(k_MLD)]
3. The level of the PBL height (k zmla ) is the level at which the maximum variation of potential temperature within the MLD exceeds some predefined threshold value: θ(k_zmla)- θmin MLD > δθ, (here δθ = 1.5 K)
4. The PBL height (zmla) is obtained using the geopotential height zg at the calculated k zmla level above the ground (zagl): zmla = zagl(k zmla ) = zg(k zmla )/g − HGT , with HGT being surface elevation height above sea level. No general rule has been applied to determine the correct value of δqv used to determine MLD. It can be determined by the namelist parameters zmlagen_dqv for δqv (default value 0.1) and zmlagen_dtheta for δθ (default value 1.5 K).

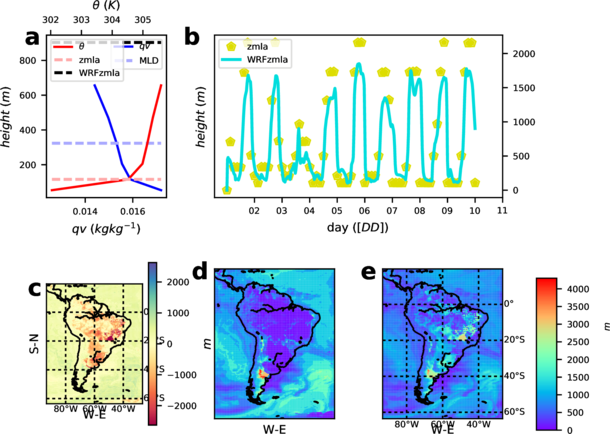
Comparison of this implementation with the zmla directly provided by WRF’s Mellor-Yamada Nakanishi and Niino Level 2.5 PBL scheme (MYNN2.5 Nakanishi and Niino, 2006) is shown in figure 1. In general the generic estimation produces a higher PBL (a panel) with lower values during night (b panel). Spatial distributions between both diagnostics are pretty similar.

Figure 1: Vertical characteristics of the atmosphere on 2012-12-09 at 15 UTC at S 62^◦ 4' 38.00", 4 ^◦ 58' 55.51" W (a): potential temperature vertical profile (θ K, red line), vertical profile of mixing ratio (qv kgkg^-1, blue line), mixed layer depth (MLD, dashed horizontal line at 323.522 m), derived boundary layer height (zmla, horizontal dashed line at 1007.122 m) and WRF derived pbl scheme value (WRF_zmla at 903.017 m). Comparison of temporal evolutions (b) between derived zmla (yellow stars) and WRF’s pbl scheme (blue line). Map of differences between derived and WRF simulated (zmla-zmla_WRF, c), zmla map (d) and zmla_WRF (e)

[editar] Convective diagnostics

Diagnostics related to convective activity are: Convective Available Potential Energy (CAPE) which accounts for all the energy that might be released convectively, Convective Inhibition (CIN) which accounts for processes which inhibit the convection, Height of the Level of Free Convection (ZLFC), Pressure at the Level of Free Convection (PLFC), and Lifted Index (LI) which accounts for the temperature difference between the environmental temperature at some higher level in the troposphere and the temperature that a parcel would have if adiabatically lifted at that level. CORDEX requires these values as statistics between output times (9freq in this case)

Since the version V3.6 of WRF, these variables can already be calculated with the module module_diag_afwa.F via the Buoyancy function. In this version of the module, this is the only available implementation. These vertically integrated diagnostics have a high computational cost. In order to minimize it, they are only computed at output time step by default.

However, if a user requires them as statistics (such as capemin, capemax, capemean), then these diagnostics are computed at all time steps. This behavior of the module is regulated via the namelist parameter convxtrm_diag (default value is 0, meaning no computation), and by setting the pre-compilation flag CDXWRF to 1 and performing some complementary modifications in module’s Registry file registry.cordex. See section 2.3 for more detail.

[editar] References

• Bergot, T., Terradellas, E., Cuxart, J., Mira, A., Liechti, O., Mueller, M., and Nielsen, N. W. (2007). Intercomparison of single-column numerical models for the prediction of radiation fog. Journal of Applied Meteorology and Climatology, 46(4):504–521.
• Brasseur, O. (2001). Development and application of a physical approach to estimating wind gusts. Monthly Weather Review, 129(1):5–25.
• Fita, L., Fernández, J., and García-Díez, M. (2010). Clwrf: Wrf modifications for regional climate simulation under future scenarios. Proceedings of 11th WRF Users' Workshop.
• Fita, L. and Flaounas, E. (2018). Medicanes as subtropical cyclones: the december 2005 case from the perspective of surface pressure tendency diagnostics and atmospheric water budget. Q. J. Royal Met. Soc., doi: 10.1002/qj.3273
• García-Díez, M., Fernández, J., Fita, L., and Yagüe, C. (2013). Seasonal dependence of wrf model biases and sensitivity to pbl schemes over europe. Q. J. of Roy. Met. Soc., 139:501–514.
• Garratt, J. (1992). The Atmospheric Boundary Layer. Cambridge Univ. Press, Cambridge, U.K.
• Hourdin, F., Musat, I., Bony, S., Braconnot, P., Codron, F., Dufresne, J.-L., Fairhead, L., Filiberti, M.-A., Friedlingstein, P., Grandpeix, J.-Y., Krinner, G., LeVan, P., Li, Z.-X., and Lott, F. (2006). The LMDZ4 general circulation model: climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim. Dyn., 27(7-8):787–813.
• Huang, H.-L., Yang, M.-J., and Sui, C.-H. (2014). Water budget and precipitation efficiency of typhoon Morakot (2009). J. Atmos. Sci., 71:112–129.
• Jourdier, B. (2015). Ressource éolienne en france métropolitaine : méthodes dâĂŹévaluation du potentiel, variabilité et tendances. Climatologie: École Doctorale Polytechnique, 2015. Français. ph:+33 01238226, pages 1–229.
• Kunkel, B. A. (1984). Parameterization of droplet terminal velocity and extinction coefficient in fog models. Journal of Climate and Applied Meteorology, 23(1):34–41.
• Monteith, J. L. (1965). Evaporation and environment. the state and movement of water in living organisms. 19th Symp. Soc. Exp. Biol, pages 205–234.
• Nielsen-Gammon, J. W., Powell, C. L., Mahoney, M. J., Angevine, W. M., Senff, C., White, A., Berkowitz, C., Doran, C., and Knupp, K. (2008). Multisensor estimation of mixing heights over a coastal city. Journal of Applied Meteorology and Climatology, 47(1):27–43.
• Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Duda, D. M. B. M. G., Huang, X.-Y., Wang, W., and Powers, J. G. (2008). A description of the advanced research wrf version 3. NCAR TECHNICAL NOTE, 475:NCAR/TNÂŋ475+STR.
• Smirnova, T. G., Benjamin, S. G., and Brown, J. M. (2000). Case study verification of ruc/maps fog and visibility forecasts. Preprints, 9 th Conference on Aviation, Range, and Aerospace Meteorlogy, AMS, Orlando, FL, Sep. 2000, 2.3:6.
• WMO (2010). Guide to meteorological instruments and methods of observation. Weather - Climate - Weather, pages

1–176.

• Yang, M. J., Braun, S. A., and Chen, D.-S. (2011). Water budget of typhoon nari (2001). Mon. Wather Rev., 139:3809–3828.

Back to the main page CDXWRF